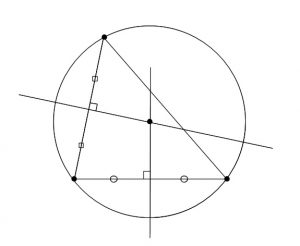
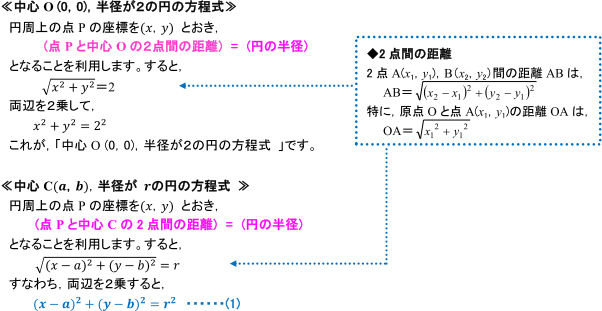
求め方 3点を通る円の中心は、その三点を頂点とする三角形の外心となる。 (求める円はその三点を頂点とする三角形の外接円) 三角形の各辺の垂直二等分線の交点がその三角形の外心となる。 外心は3つの頂点から等距離にある。 その外心から各点の頂点の距離が円の半径となる。 外心の求め方例題 上節でみたように,$2$ 円の位置関係を調べるには,$2$ つの円の半径と,中心間の距離を調べればよいのでした.円の方程式からその中心の座標と半径を求める方法は前記事 →円の方程式の表し方 で紹介しています.これらの知識を用いて,実際にいくつかの例題を解いてみましょう.右図4は原点を中心とする半径5の円のグラフであるが,この円は縦線と2箇所で交わるので,1つの x に対応する y が2つあり,円の方程式は1つの陽関数では表せない. 右図5において,原点を中心とする半径5の円の方程式を求めてみよう.

基本 2つの円の共有点 中心間の距離に注目 なかけんの数学ノート
円 中心 求め方 2点
円 中心 求め方 2点- 円の中心を求める まずは、中心を求めたい円の周上にコンパスの針の部分を置いて、 少し大きめの半円を書くよ 周上の他の場所にも、コンパスの針を置いて さっきと同じ大きさの半円を書くよ そして、半円2つが重なった2点を結ぶ線を引くよ 最後に、もう1つ他の周上にコンパスの針を置いて半円を書くよ また線を書いて、 放物線 y = x^2 に二点で接する円の中心が y軸上にあることは 自明であるか, という所の問題ですね 入試で出すなら, y軸上に中心を持つ円を考えることを問題に明示 することでしょう 「放物線 y = x^2 に二点で接する円の中心が




2点間の距離 内分 外分する点の座標の求め方 数学の偏差値を上げて合格を目指す
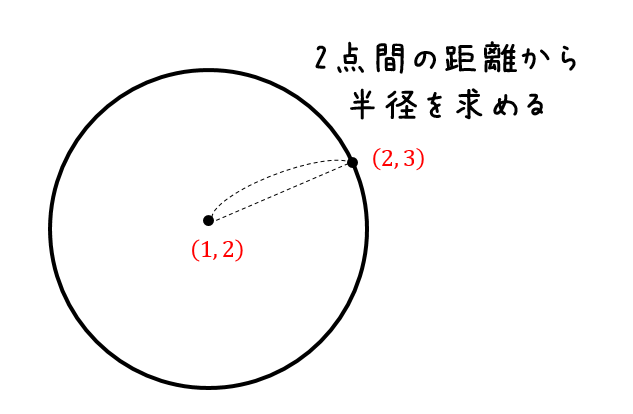
円の中心が点 \(\mathrm{A}(a, b)\)、半径が \(r\) の円の方程式は \begin{align}\color{red}{(x − a)^2 (y − b)^2 = r^2}\end{align} 特に、原点が中心 \((0, 0)\) で、半径が \(r\) の場合は \begin{align}\color{red}{x^2 y^2 = r^2}\end{align}中心角とは 次に、中心角について解説していきます。 中心角を一言で言うと、円周角の中心バージョンです。 円周角では、点を円周上に3つ置きましたが、円周上に2つ置いた点と、円の中心をそれぞれ結んだときに出来た角を中心角といいます。 これを 同じようにポイントを2点決定して直線パスを作成します。 今回は検証用に片方のポイントを同じにします。 先ほどと同じように、直線パスの回転&コピーと拡大を行っておきます。 直角に回転したパスの交わるところが円の中心になっているはずです。
動画による解答は以下になります 数学円の接線の方程式の求め方(解法③:接点を求めて計算量を軽くしたい)高校 数学 図形と方程式 数学2(質問ありがとうございます! ) では実際にやってみましょう! 点(4, 6)を通り、円 (x -1)2 (y - 1)2 今日は、任意の3点座標から円の中心座標を求める方法デスw 先ず、 ・任意の3点で円が描画できるw ・円の中心までの距離は同じ(半径)w ・2点間 (a,b) (c,d) の距離を求める計算式・・ 上記の写真を例に円の中心座標を求めてみるw2点u, vを固定したとき, この2点を通る円の中で 包含円となりうるものは何通りあるか? u v 赤側 青側 u, v以外の点を直線uv に 関して2分割 赤側と青側 各点について,その点と u, vを通る円を求めたとき, 青側の点は,青側に中心 をもつ半径最大の円の 内部
2点と半径から円の中心を求める 2点の座標と半径を入力すると、指定した半径で2点を通る円の中心座標が表示されます。 2点間の距離 < 半径×2 → 中心が2つ 2点間の距離 = 半径×2 → 中心が1つ(1点目と2点目に同じ座標が表示される) 2点間の距離 > 半径×2円の半径とは、円の中心から円周上の任意の点を結んだ線の長さです。 半径を最も簡単に求める方法は直径を2で割ることです。 直径がわからなくても、円周 ( C = 2 π r {\displaystyle C=2\pi r} )や円の面積 ( A = π r 2 {\displaystyle A=\pi r^ {2}} )など他の値が与えられすなわち,上記の偏心(a,b)を決定し,それを中心と した同心円でワーク形状を挟んだ場合の半径差が真円度と なることを意味している. 5.真円度と基準円 真円度の求め方には,基準円を元に以下の4つの方法が ある3). 1.最小領域真円度/最小領域基準円




2つの円の位置関係と共通接線の求め方 図形と方程式 2



3次元空間での円の中心の求め方 Inak Engineering Llc
円の中心、半径の求め方 中心の座標と半径を求めるためには、円の方程式を次の形に変形する必要があります。 こうすることで、中心と半径を読み取ることができます。 というわけで、円の方程式を変形していきます。 まずは、並べかえて と をまとめます。 次に と について、それぞれ平方完成していきます。 平方完成ができたら、残りモノは右辺に移行しよって求める点Pの軌跡は 放物線 となります。 (2) の中心 p の軌跡を求めます。 与式を円の方程式 の形に変形します。 ※ 円ならば右辺は半径の二乗なので 0 より大きな値になるはずです。 右辺の平方完成をすると、 となり、円の条件を満たします。 設定 2次元平面上の2点を与えられた時、そこを通る円が存在するなら2つある その円の中心2つを求めたい 解法 2次元ベクトルで考える(プログラム的には複素数complexを利用する) 2点の中央cから垂直方向に単位ベクトルnを考える(画像参照) それを長さx分だけ伸ばしたところが円の中心で、x




円の方程式の求め方まとめ パターン別に解説するよ 数スタ




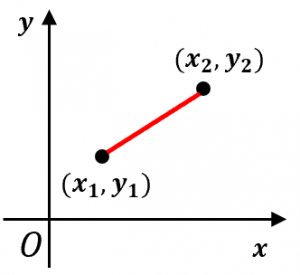
2点間の距離の公式を証明と例題でわかりやすく解説 立体の場合の計算方法も 高校生向け受験応援メディア 受験のミカタ
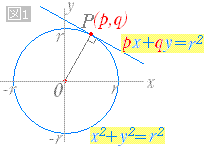
(1)該当円の接点(母点)3点の内、2点の母点を共有するすべての円の中心点を求め、 中心点を結ぶ線がボロノイ辺となります。 (2)該当する円がない場合は、該当2点の母点を結ぶ2等分線がボロノイ辺の一部となります。 (該当円の中心点から、母点が存在しない方向に引いた線がボロノイ辺と円上の任意の点の極座標を (r, θ) とし、中心の極座標を (r0, φ) (つまり、中心の原点からの距離が r0 で、 φ は原点から中心へ結んだ半直線が、 x 軸の正の部分から反時計回りになす角)とするとき、半径 ρ の 円の極方程式 は r 2 − 2 r r 0 cos ( θ − φ ) r 0 2 = ρ 2 {\displaystyle r^ {2}2rr_ {0}\cos (\theta \varphi )r_ {0}^ {2}=\rho ^ {2}} と書ける。原点以外中心・円外の点があたえられたときの一例 ①接線の傾きをm として、 p q, を通る直線の 方程式y q m x p を作る ②①の式を一般形に変形して、円の中心との距離d を求める ③②で求めた距離d と円の半径r が一致する(d r )ときの 傾きm を求めて,接線を




高校数学 円外の点から引いた接線の方程式 受験の月




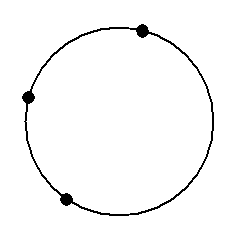
中学数学 3点を通る円の中心の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
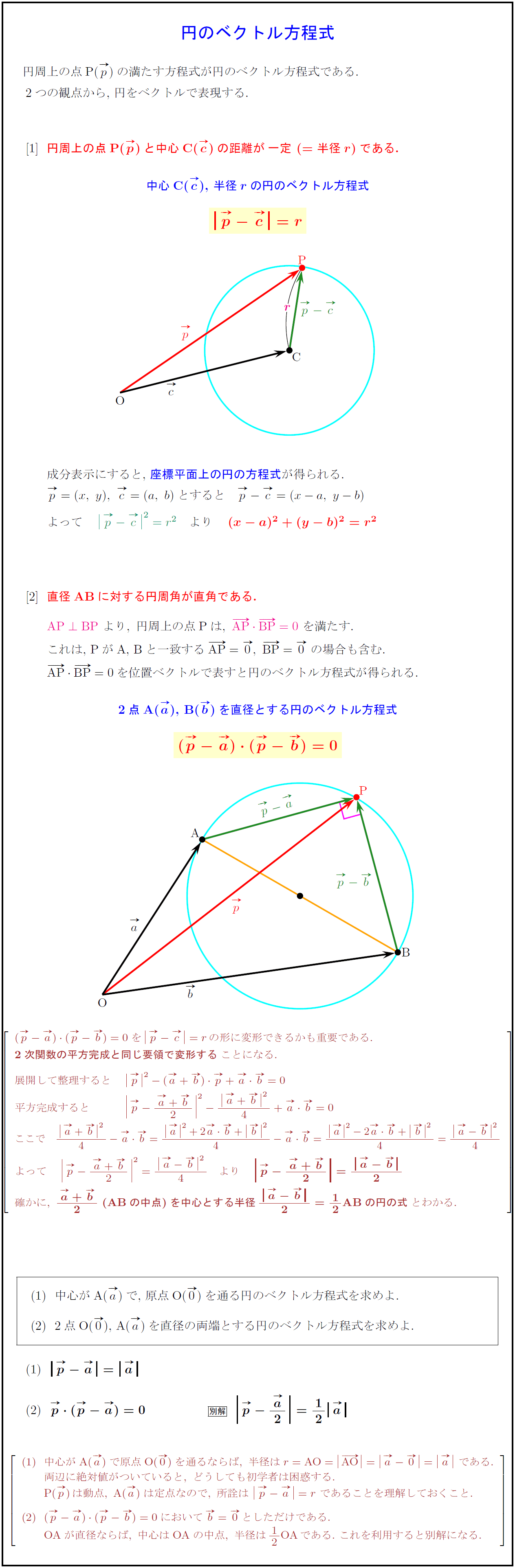
四角形の重心の2通りの求め方と注意点 等周問題に関連する高校数学の問題 図形の対称移動・グラフの対称移動 円の方程式と関連問題|座標・ベクトル・複素数 平面,空間上の2点間の距離について リサージュ曲線の定義とそれに関連する話 そいつと被らない円周上の2つの点を、 簡単計算!2つのサイコロの確率の求め方がわかる3ステップ 中3 >弧の長さが2倍、3倍・・・になると、円周角・中心角も2倍、3倍・・・になるのですか? 異なる2点で交わる場合の交点の求め方の考え方 円の中心を $C$ 、2つの交点を $A,B$、点 $C$ から直線に向かって下ろした垂線と直線との交点を $H$ とすると、 点 $C$ から点 $A$ に向かうベクトルは、 $$\overrightarrow{CA}=\overrightarrow{CH}\overrightarrow{HA}$$ となる。 よって、点 $A$ の座標は、点 $C$ の位置ベクトルを $\vec{c}$ とすると、




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



円の方程式の公式は 3分でわかる意味 求め方 証明 3点を通る円の方程式
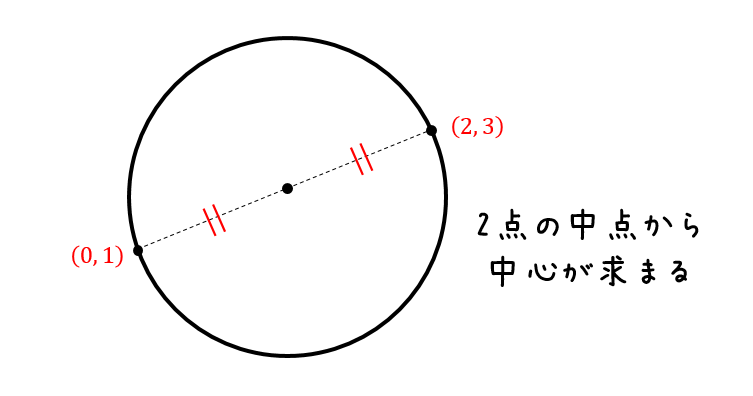
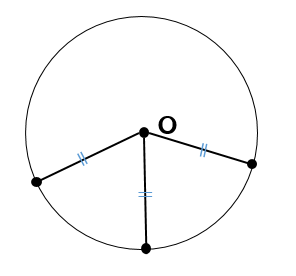
指定した3点を通る円の式 困っていたのでありがたいです。 計算過程も書いてあると尚嬉しいです。 タンクの中心からずれた位置へ差し込むパイプの長さを求めました。 半径rと x座標a,c,e から y座標b,d,f が求められればサイコーです! アンケートにご2、紙に書いた円にピッタリと角が合うように 直角の物(ハガキなど)を置きます。 (Pの位置) 3、直角の物と円が交わる2点に印を付けます。 (AとB) 4、AとBを結んだ線の真ん中の点が、この円の中心になります。 (Oの点) 5、紙を空き缶に乗せて、求めた円の中心をクギなどで印を付ければできあがり! これは、 円周角の定理 を使った円の中心の求め方 だから円の中心は三角形の各辺の垂直二等分線の交点になります。 幾何で知っていると思いますが垂直二等分線は2本で良いですよ。 3本目の交点も必ず一致しますから。 垂直二等分線の方程式を2本求めて連立すれば中心が求まるということです。




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




この問題の の中点の座標の求め方を教えて下さい 至急です Clear
2点と半径で円の中心が決まるのはごく簡単です。 こんな感じですね。 さて、当然の事ながら2次方程式の解ですので答えは最大2つ出てきます。 上図が一つの答えですが、この2点を通る中心位置が違う円がもうひとつあるのはすぐわかりますね。 二点を通る円で半径Rの円の中心点を求めるには、 が正しい書き方です。 2点を(x1,y1),(x2,y2)とし円の中心点を(x,y)と置くと次の式が成立する。 (xx1)^2(yy1)^2=R^2 (1) (xx2)^2(yy2)^2=R^2 (2) (1)(2)から (2xx1x2)(x2x1)(2yy1y2)(y2y1)=0 (3) 計算フォーム Excel用フォーマット 導出 円の方程式 円の中心 円の半径 別解:垂直二等分線の交点を計算 計算フォーム計算結果だけ知りたい場合は,次の計算フォームを利用してください(*1): 1点目 $x_1=$ $y_1=$ 2点目 $x_2=$ $y_2=$ 3点目 $x_3=$ $y_3=$ 中心$(a,b)=$ 半径 $r=$ // Excel用フォーマット



円の方程式の求め方まとめ パターン別に解説するよ 数スタ




円の方程式 数学ii フリー教材開発コミュニティ Ftext
曲率・曲率半径の感覚的な意味と求め方 レベル ★ 最難関大受験対策 極限,微分 更新日時 曲率半径 とは,曲線を「局所的に円の弧」とみなしたときの円の半径。 曲率 とは,曲率半径の逆数。 曲率・曲率半径について解説します。 曲率半径 球の中心の求め方 前回のコラムで3次元空間での円の中心の求め方について記述したので、次に空間内にある球の中心を求めるロジックについて考えてみます。 球については、表面上にある4点の座標が指定されたら形状が確定します。 (3点の座標と半径⇒ 「3点を通る円」と「2点とある直線上に中心がある円」の方程式の求め方 いろいろな解法が思い浮かぶのは、図やグラフを書いているからですよ。 ⇒ 図形と方程式の要点 単元毎のまとめですが全体を見渡しておく方が理解しやすいです。




高校数学 3点を通る円の方程式の決定 練習編 映像授業のtry It トライイット



3点を通る円 と 2点とある直線上に中心がある円 の方程式の求め方
まず、点Aと点Bにコンパスの針を置いて 同じ半径を持つ円をそれぞれかきます。 そして、2つの円が交わったところを線で結べば完成です! 簡単ですね! 覚えておきたいポイント 円の中心は、円周上のどの点からも距離が等しい。 垂直二等分線を作図することで2点から等しい距離にある点を作図できる。 垂直二等分線の作図方法 2点にコンパスの針を置いてでは,円の方程式の導き方を確認しましょう。 ここでは,『「円周上の点」と「中心」の距離』と『半径』が同じということを利用して,円の方程式を導いてみます。 さらに,この式を展開して整理すると, x 2 y 22ax2bya 2 b 2r 2 =0 となります。2円の交点を通る円・直線の方程式の 解説 2つの円 x2y2axbyc=0 (1) x2y2dxeyf=0 (2) が2点で交わるとき,方程式 x2y2axbyck(x2y2dxeyf)=0(A) は,定数 k の値にかかわらず2交点を通る円を表す.



幾何計算 2点と半径から円の中心点を求めます Satoh




3点を通る円の方程式を簡単に求める方法とは 大学入試数学の考え方と解法
二つの円の接線の求め方 2つの円の接線を作図する方法を以下に示します。 二つの円と距離を定義 2つの円の半径をr、r'中心間の距離をlと定義します。 r o r o' l 接線との平行線を作図 半径rの円と同心円の半径rrの円を作図します。(57)要約 目的 円周上にゴミや欠けがある場合にもこれらの 影響を取り除き、高精度で円中心位置を求める。 構成 二次元の画像データからエッジ点を検出する 工程と、エッジ点の集合について平均四乗誤差最小化法 によって円弧近似を行い円中心の位置を推定する工程 と、推定さ今回必要な、円の中心と円の中心との距離を求めるためには、 三平方の定理が必要になります。↓を見てください p1,p2をそれぞれ、円の中心だとすると、円の中心間の距離dは d^2 = (px2 px1) × (py2 py1) とういうことになります。




基本 2つの円の共有点 中心間の距離に注目 なかけんの数学ノート



円の方程式の求め方まとめ パターン別に解説するよ 数スタ
(1) 直線lの式を求めなさい。 (2) 点Q の座標を求めなさい。 (3) 線分AP を直径とする半円をAP の上側にかくとき, この半円とy 軸との交点の座標を求めなさい。 8 右の図のように,点C(0,10)を中心とする半径6 の円に,



円の方程式の導き方 数学 苦手解決q A 進研ゼミ高校講座




2点間の距離 内分 外分する点の座標の求め方 数学の偏差値を上げて合格を目指す




この求め方でも大丈夫ですか Clear
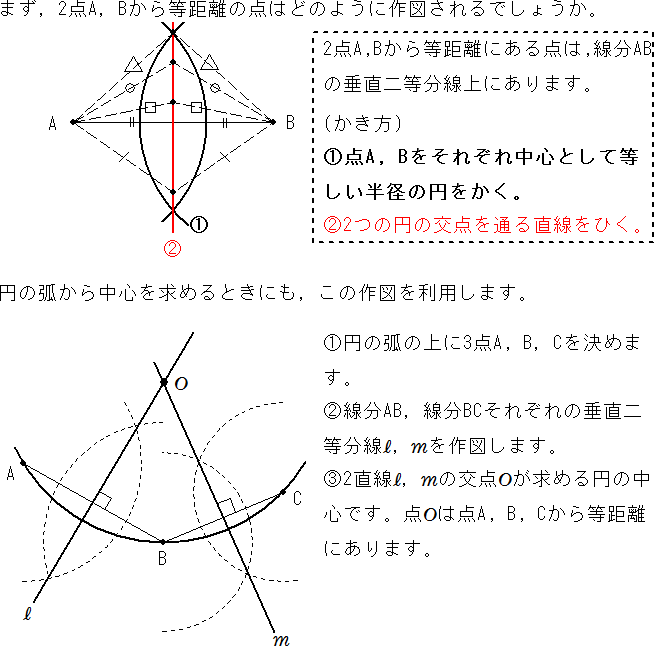



平面図形 円の中心を求める作図 中学数学 定期テスト対策サイト



円の接線の方程式




球面の方程式の求め方と問題の解き方をわかりやすく




3分でわかる 点と直線の距離の公式の証明 使い方のコツを分かりやすく 合格サプリ



二点間の距離を求める公式 2次元 3次元 具体例で学ぶ数学



高校数学b 円のベクトル方程式2パターン 受験の月



外接円 外心について



幾何計算 2点と半径から円の中心点を求めます Satoh



円と直線の交点を求める Qiita



円 数学 Wikipedia




2つの点から円の方程式を求める 数学ii By Okボーイ マナペディア



幾何計算 2点と半径から円の中心点を求めます Satoh
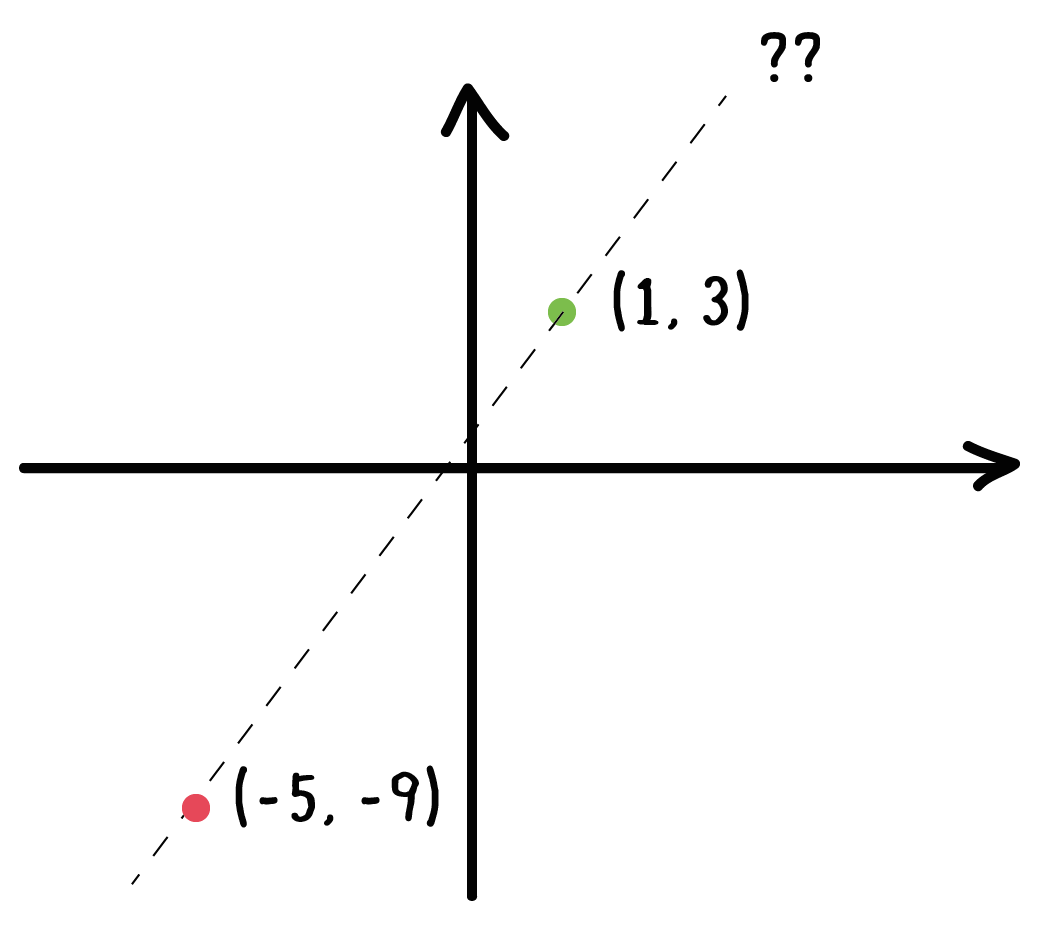



1次関数 2点を通る直線の式の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




2点間の距離の公式を証明と例題でわかりやすく解説 立体の場合の計算方法も 高校生向け受験応援メディア 受験のミカタ
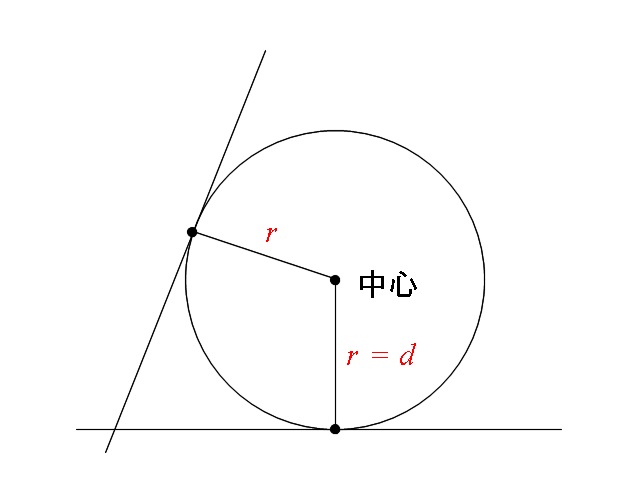



円に接する直線 接線の方程式 の求め方3パターン



1
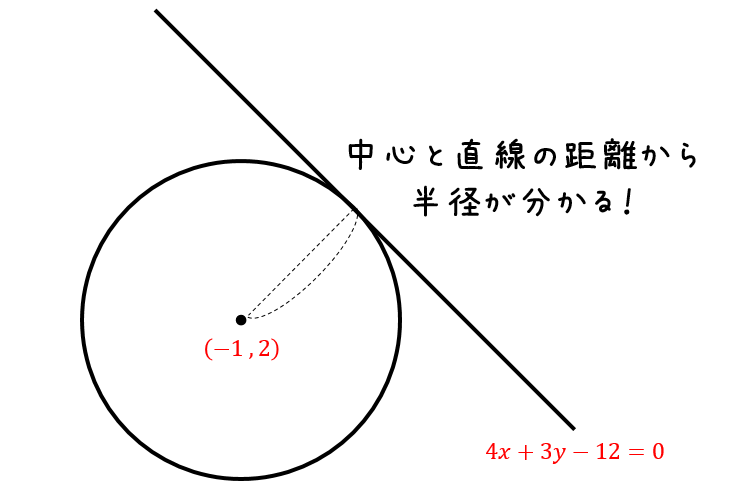



円の方程式の求め方まとめ パターン別に解説するよ 数スタ



2 つの円の位置関係 思考力を鍛える数学




画像にある各座標の求め方について こちらの図で 点a B Cの座標の求め Okwave




円の方程式 数学ii フリー教材開発コミュニティ Ftext




垂直二等分線を使って円の中心をもとめる 中学数学 By Okボーイ マナペディア



Studydoctorさまざまな円の方程式の求め方 高校数学 Studydoctor
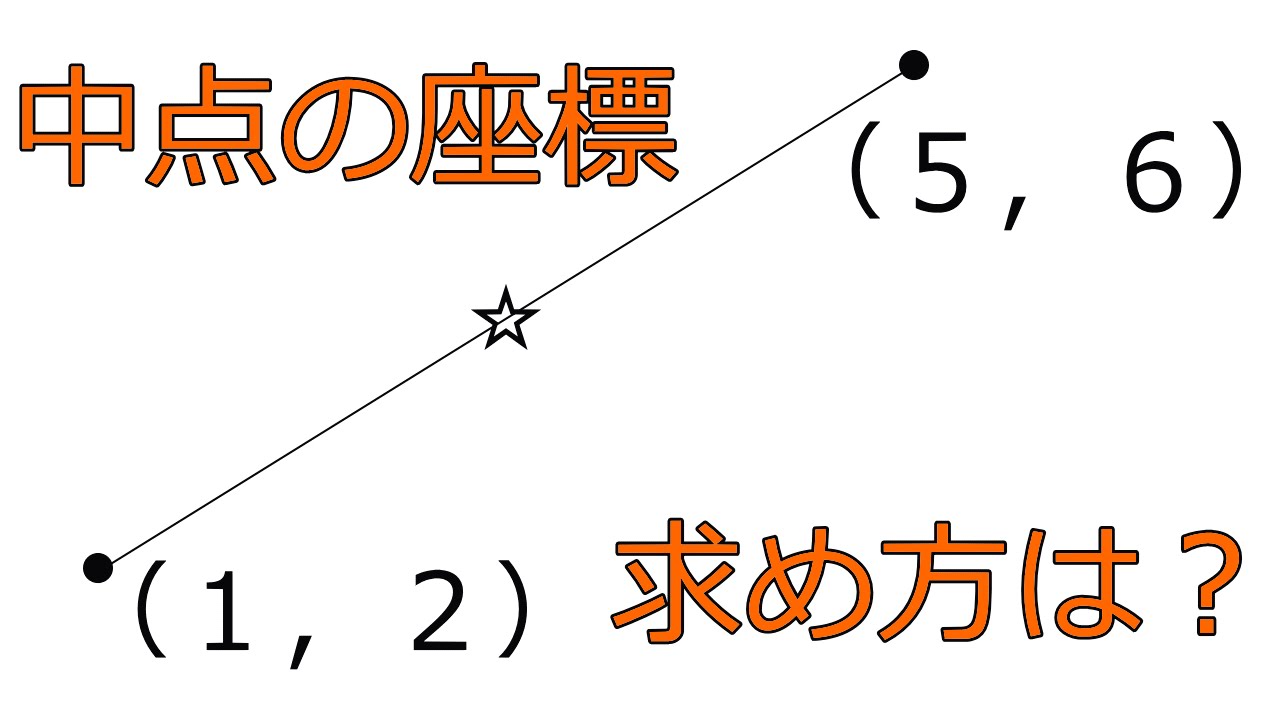



中点の座標の求め方 中学1年数学 Youtube




円の中心を求める 3つの方法 Wikihow
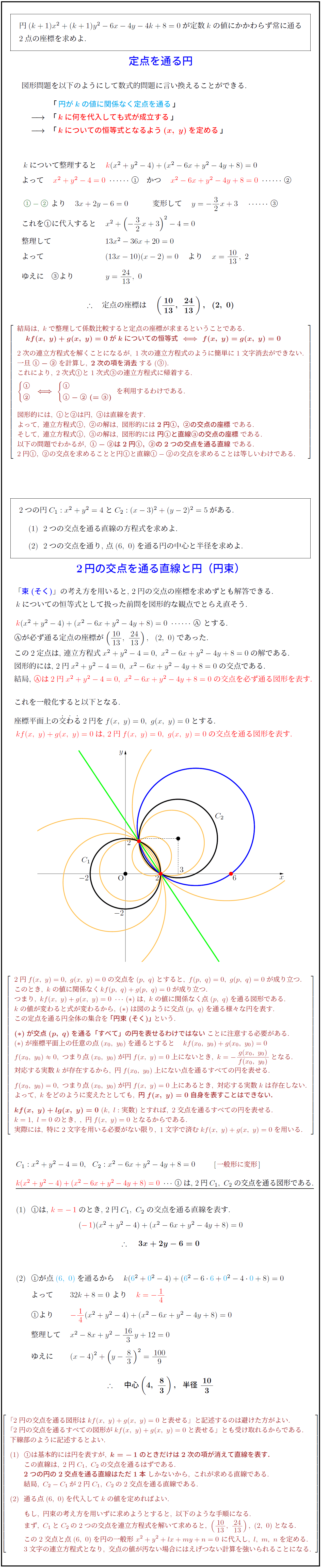



高校数学 定点を通る円 2円の交点を通る直線と円 円束 受験の月
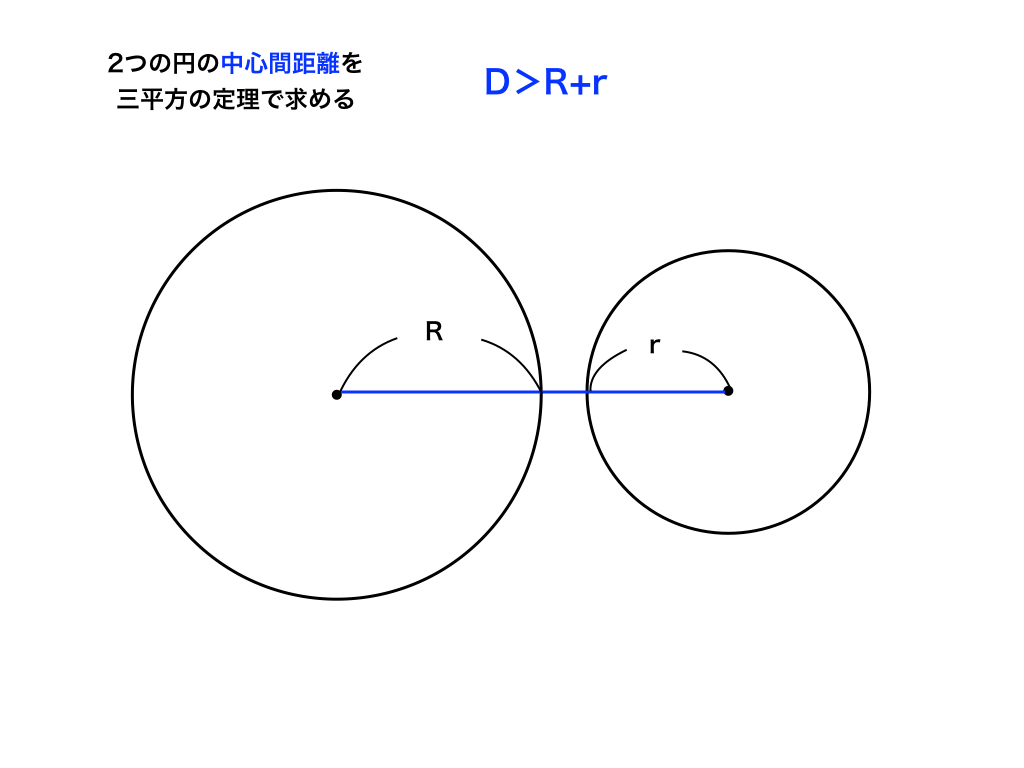



2つの円の位置関係と共通接線の求め方 図形と方程式 2




円の中心を求める 3つの方法 Wikihow
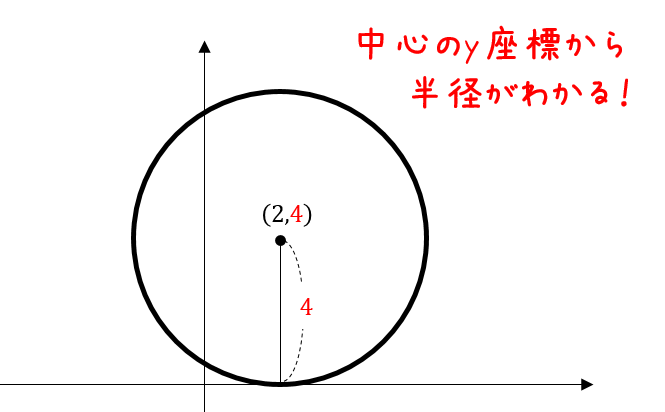



円の方程式の求め方まとめ パターン別に解説するよ 数スタ




円と直線の交点を求める Qiita




円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト
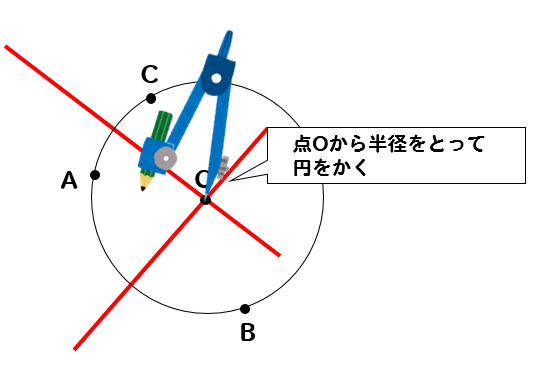



中1 作図 円の中心を求める方法を解説 数スタ




垂直二等分線を使って円の中心をもとめる 中学数学 By Okボーイ マナペディア




円の中心を求める 3つの方法 Wikihow




円の中心の作図 コンパスを使って求める方法とは 中学数学 理科の学習まとめサイト



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典
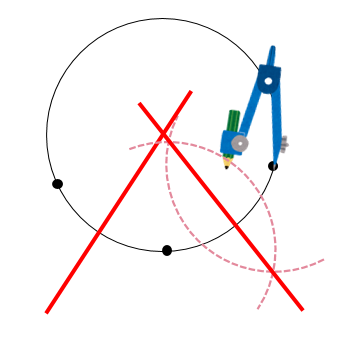



中1 作図 円の中心を求める方法を解説 数スタ



2 つの円の位置関係 思考力を鍛える数学



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典



中1 作図 円の中心を求める方法を解説 数スタ



通る2点と半径が分かっている円の中心の座標ってどう求めればいいんでし Yahoo 知恵袋



幾何計算 2点と半径から円の中心点を求めます Satoh




高校数学 点と直線の距離の公式 映像授業のtry It トライイット



1



数学の質問です 中心が点 1 2 で 円x 2 Y 2 に内接する円 Yahoo 知恵袋




円の中心を求める 3つの方法 Wikihow




Processing 2点を通る直線と円の交点を求めよう Zawaworks S Diary



外接円 外心について




問題 2つの円 X 2 2 Y 1 2 4 の交点p Qを通る直線の方 人力検索はてな



円の中心の求め方 Love金沢水彩画



幾何計算 2点と半径から円の中心点を求めます Satoh




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室
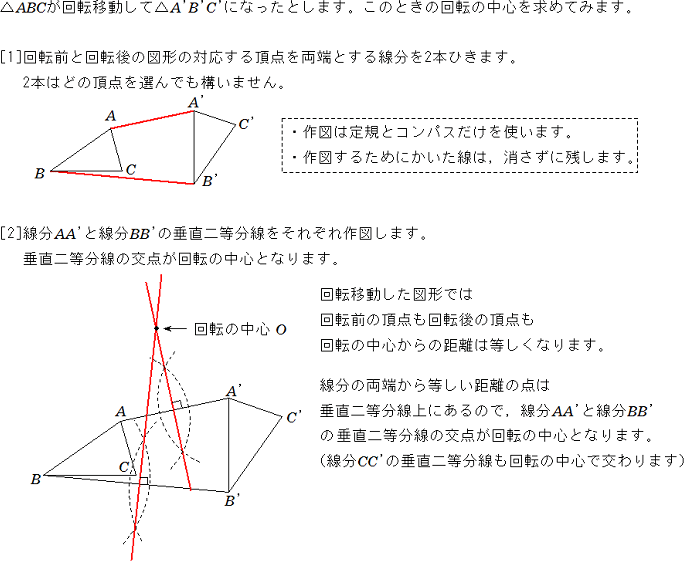



平面図形 回転の中心の求め方 中学数学 定期テスト対策サイト




2つの円の位置関係と共通接線の求め方 図形と方程式 2




作図により円の中心の求める方法について質問です ある円で任意の異 数学 教えて Goo
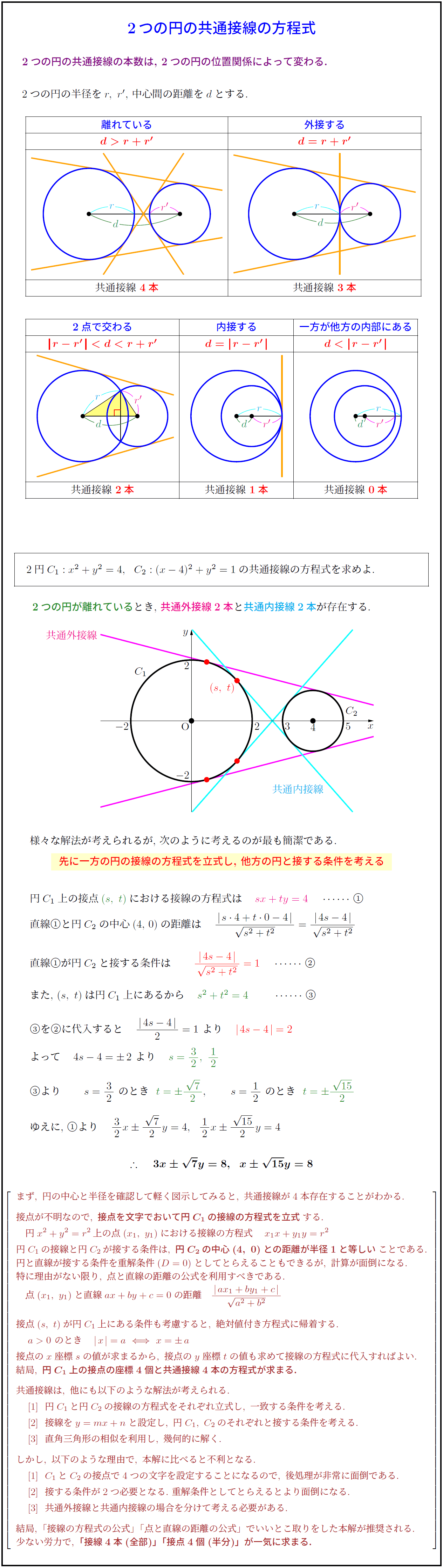



高校数学 2つの円の共通接線の方程式 受験の月
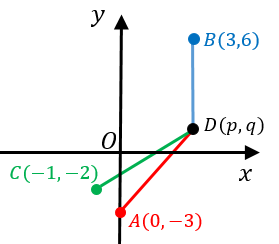



3点を通る円の方程式の2通りの求め方と検算方法 具体例で学ぶ数学




Processing 2点を通る直線と円の交点を求めよう Zawaworks S Diary




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室




3 が分かりません どうやったらマーカーで引いてる式が でるのですか Clear



3点を通る円 と 2点とある直線上に中心がある円 の方程式の求め方



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




円の接線の方程式とその証明 おいしい数学




応用 2つの円の交点を通る円や直線 なかけんの数学ノート



円の方程式の公式は 3分でわかる意味 求め方 証明 3点を通る円の方程式
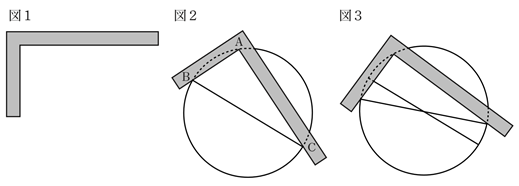



曲尺を使い円の中心を求める 1 準2級 カワズの数学ノート 数学検定 準2級
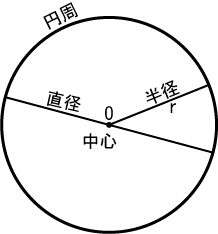



円 数学 Wikipedia




基本 円の方程式 なかけんの数学ノート




6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4
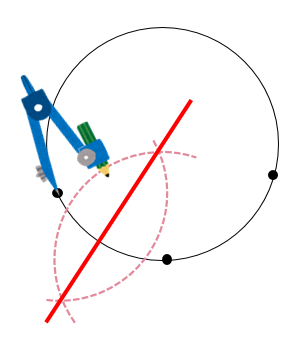



中1 作図 円の中心を求める方法を解説 数スタ




中学数学 円の中心の出し方 コンパス編 サクッとわかる なぜか分かる はかせちゃんの怪しい研究室



1
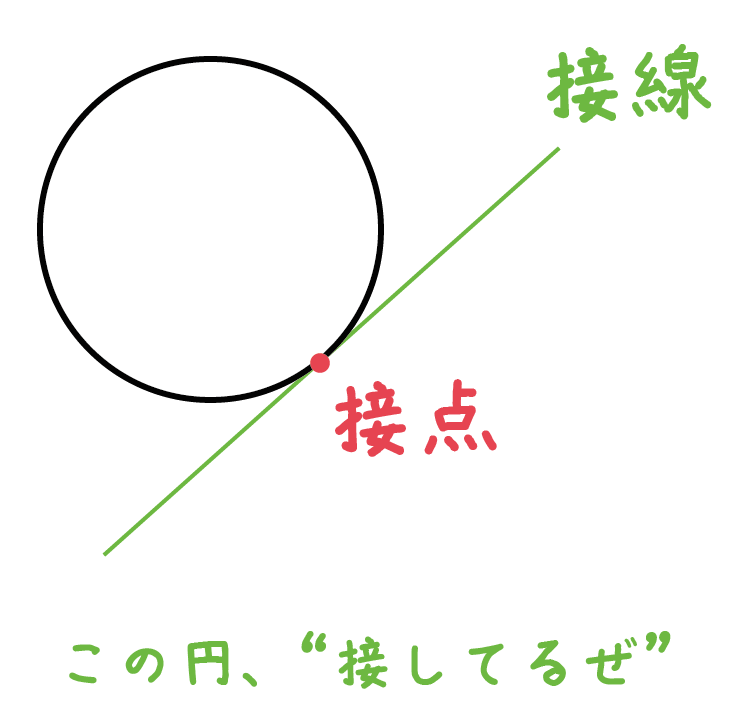



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく




任意の3点を通る円を求める方法 プログラマーのメモ書き




中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
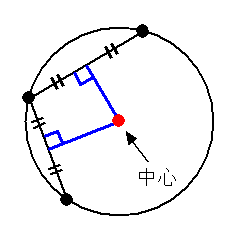



3次元空間での円の中心の求め方 Inak Engineering Llc
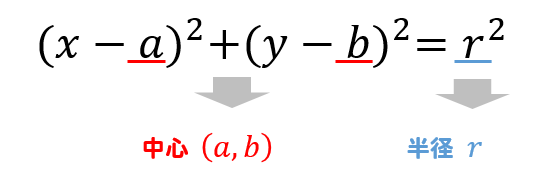



円の方程式 中心の座標と半径の求め方を解説 数スタ



Q Tbn And9gcs8govrxmmsri Uq2ku4tuxauhmioafyuowrywnpq8yleyditf9 Usqp Cau




作図により円の中心の求める方法について質問です ある円で任意の異 数学 教えて Goo
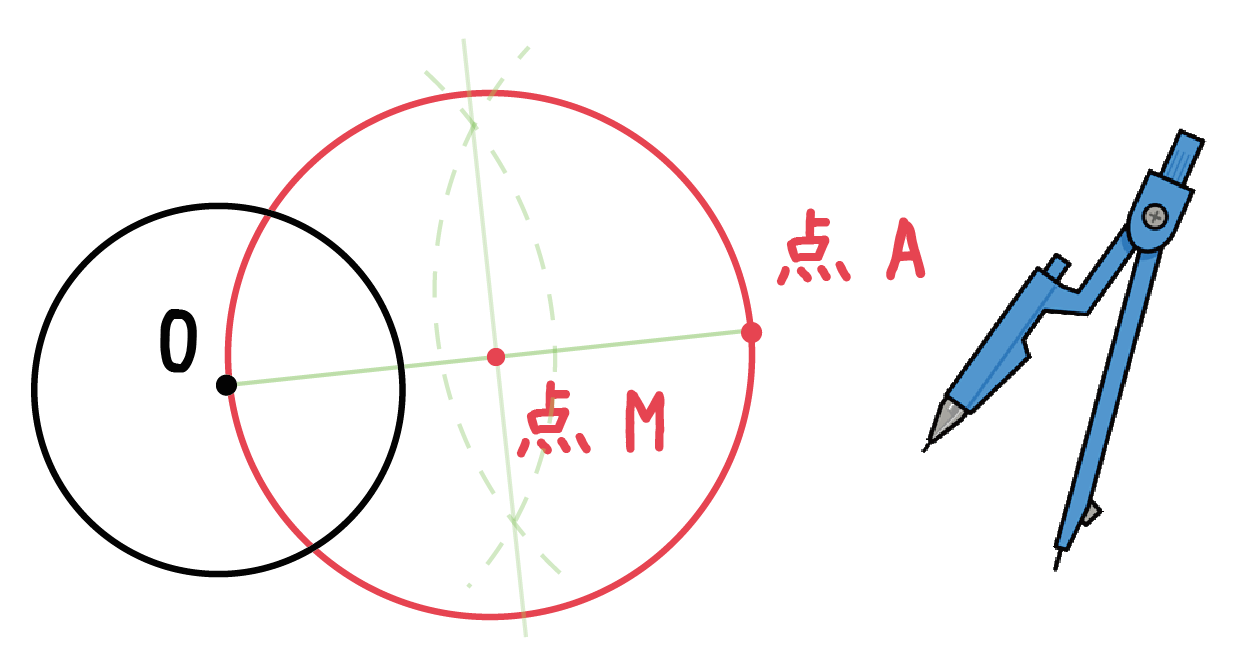



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく



円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典




基本 2つの円の共有点 中心間の距離に注目 なかけんの数学ノート




高校数学 円と直線の位置関係の分類 映像授業のtry It トライイット



0 件のコメント:
コメントを投稿