A=B=CをA=C, B=Cの形にして2つの式にする。 2x5=7x3y9 2y13=7x3y9 2x5=7x3y9を 整理して5x3y=4 2y13=7x3y9を 整理して7x5y=4 5x3y=4の両辺に5をかけ、7x5y=4の両辺に3をかけ、辺々引くと 25x15y = ) 21x15y = 12 4x = 32 両辺を4で割る三元連立方程式 自分の計算が不安で利用させていただきました。 思っていたより間違ってたので使ってよかったです。 4元にも対応してくれたら大変有難いです。 世界の経緯度観測所のデータ(3か所)から、形状軸からの極 (瞬間自転軸)のズレの計算に使用しました。 今度はエミルート行列の勉強をします。 煩雑な手計算分、入力から出力まで1分。 大変 連立方程式の解を求めるための具体的な方法として、加減法と代入法の二つの方法がある。 連立を組んでいる全ての方程式が受け入れられるものが連立方程式の解になる。 一部の方程式を満たすだけでは連立方程式の解とはいえない。 menu 検索 最近の投稿 期間限定配布!「電験3種教

大家來解謎 解二元一次聯立方程式 導入活動 環遊數界
3連立方程式 解き方
3連立方程式 解き方- 掃き出し法による3元1次連立方程式の解き方の手順 準備が整ったところで、いよいよ3元一次連立方程式の解き方に入ります。 今回は次の3元一次連立方程式を例として解説していきます。 2xy3z=6 x3y2z=1 3x2yz=7 正則行列であるか行列式を求めて確かめる抵抗に関する連立方程式を解く必要がある。そこで,「キルヒホッフの法則」を説明する前に,ここ では数学的な準備として,未知数が二つの2 元連立1 次方程式と変数が三つの3 元連立1 次方程式に ついて,クラーメルの公式による解法を説明する。 1 2元




均一影片 例題 解二元一次聯立方程式 綜合應用3 學習單 Shareclass
3 連立1次方程式 次の連立1次方程式を考える。1 a11x1 a12x2 ·· a1nxn = b1 a21x1 a22x2 ·· a2nxn = b2 am1x1 am2x2 ·· amnxn = bm (1) 行列を用い、方程式(1)は、次の行列の方程式でも表される。 a11 a12 ··a1n a21 a22 ··a2n定義 28 (連立一次方程式の基本変形) 連立一次方程式に対する次のの操作を 連立一次方程式の基本変形と呼ぶ. (1) 一つの式を 倍する. (2) 二つの式を入れ替える. (3) 一つの式を 倍して別の行に加え 第3回 連立方程式のアピール(前編) お気に入りに追加 ;
連立方程式 濃度に関する問題その3 calendar 17年02月14日 reload 17年04月10日 folder 福島県高校入試対策(17)33連立 1 次方程式の基本変形 定義 38(連立 1 次方程式の基本変形) 連立 1 次方程式に対する次のの操作を連立 1 次方程式の基本変形と呼ぶ. (1) 一つの式を 倍する. (2) 二つの式を入れ替える. (3) 一つの式を 倍して別の行に加える. 連立 1 次方程式に基本変形をして得られた方程式と元の方程式とは等価な方程式である.3 1 連立方程式の表現方法 連立1次方程式 (Linear Equations)は,次のような形をしている. 式 ( 7 )は行列とベクトルで書くと,式がすっきりして 考えやすくなる.書き直すと, ( 8) である.それぞれの行列とベクトルは, を表す. 通常,連立1次方程式 ( 7 )は と書き表せる.このようにすると,見通しがかなり良くなる.
2元1次方程式や連立方程式の意味を理解し、代入法や加減法で、連立方程式を解く練習をする問題プリントです。 連立方程式の解き方 練習問題 (1) 答え 連立方程式の解き方 練習問題 (2) 答え 連立方程式の解き方 練習問題 (3) 答え 連立方程式の問題391 複素数を表す変数x,y,z に関する次の3元連立方程式を解きなさい: 3x−6y5z=5 4x2y−z=1 7x−4y8z=2 連立方程式を構成する方程式のうちの片方が1次方程式で他方が2次方程式である ときを扱います. 例題 複素数を表す変数x,y に関する次の連立方程式を解く: ˆ 3x−2y−1=0 2y2−3x2 =3y−4x5 連立方程式の裏技です📢 暗算が得意!って方にオススメです☆ 数字が大きいときに使うのは向いていません(1075×16とか出てきても筆算に時間がかかるだけなので)。 でも、すぐに積が分かりそうなら絶対に裏技を使いましょう!時間短縮になりますよ🙌 ぜひ覚えて使ってみてね〜 学年



第1章 連立方程式




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download
3 連立1次方程式(1) 筑波大学オープンコースウェア|TSUKUBA OCW 18年度 数値計算 3 連立1次方程式(1) 文字が3つ出てくる連立方程式の解き方 ここまでの連立方程式はすべてxとyという2種類の文字しか出てきませんでしたが、実際は文字が2つとは限りません。 以下の問題を考えてみましょう。 問題x, y, zの値を求めよ。 xyz = 6 3x2yz = 10 x2yz = 6 解説 文字が3つでも、やることは変わり== 連立方程式の解き方 == この頁では,未知数の個数と方程式の個数とが等しい(*)ような連立1次方程式の解き方を扱う.さらに,係数行列に逆行列が存在する場合(**)だけを扱う. 内容的には, (1)筆算により代数的に解く方法を簡単に振り返り (2)Excelで解く方法 (3)wxMaximaで解く方法 を使って
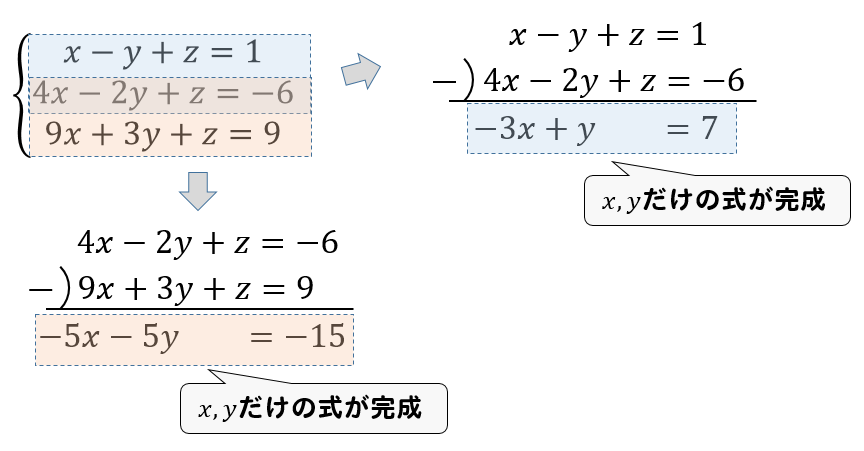



連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト




均一影片 例題 解二元一次聯立方程式 綜合應用3 學習單 Shareclass
3つの文字、式の連立方程式を計算する方法 xy=3,xy=2の和と積の連立方程式の解き方は? 途中で速さが変わる文章問題の解き方、コツを解説! 割合を使った全校生徒の増減に関する文章題の解き方を解説! 池の周りを追いつく速さの問題を解説!Rとの連立方程式を解く (3) 次の式があるとします。 x 2y 3z = 2x 5y 9z = 100 5x 7y 8z = 0 これらの方程式をx 、 y 、 zについてどのように解くべきですか? 可能であれば、Rやその他のコンピュータツールを使って、これらの方程式を解きたいと思います。3.連立1 次方程式の解法 4.解の分類と図形 5.おわりに 1.平面上の直線 xy平面上の直線の式を復習しておく. (a) 定点を通ってベクトルnに垂直な直線 平面上で定点P0 とベクトルnが与えられたとする (図11).P0 を通ってn に垂直な直線g の式は以下 のようにして決まる.まず,原点をOとし




方程式計數機連立一次方程式の計算機 Cpdpg




2次関数26 連立3元1次方程式 怜悧玲瓏 高校数学を天空から俯瞰する
図3 ソルバー:パラメータ設定画面 図3の実行ボタンをクリックすると、図4のように解が算出される。 図4 ソルバーの実行結果 図4より、 Ax = b となっています。 これで、連立方程式の解が求まった。この頁では,主に連立方程式の「掃き出し法」による解き方(または「行基本変形」による解き方,または「ガウスの消去法」による解き方)を扱います. 全体の流れ 未知数2個,方程式2個のとき 次の連立方程式において,未知数 x を消去したいとき,(1)式のように≪ x の係数が 1 x の一つの行列の等式は,その成分数だけの連立方程式と同じです。 例1: = は,連立方程式 a=1 b=0 c=0 d=1 と同じです。 例2: は,連立方程式 x=3 y=4 と同じです。 例3: は,左辺を計算して2×1行列にしておくと ax+by=p cx+dy=q と同じです。 (ア) の両辺に左からA1 を掛ける




隨筆誌 二下2 3三元一次聯立方程式比例式解題想法




整数解をもつ連立3元2次方程式を解こう 2017年度前期日程の一橋大学入試問題 身勝手な主張
この例題の,(35)式の形に至るまで(すなわち,解がそれぞれ求まるまで)3つの演算を行う 解法を GaussJordan の消去法という.消去法は,変数の数が増えても有効な解法である. ところで,連立1次方程式(31)を行列の式で表すと第3回連立方程式の一般解 本日の講義の目標 目標3 1 連立方程式の解をパラメータを用いて表す方法について理解する 2 連立方程式に解が存在しない場合の扱いについて理解する 23/98 連立方程式とパラメータ 前回習った方法(基本変形) を次の方程式に適用すると, 係数行列を単位行列まで 変形連立方程式を解け 3 (2xy)=3x7y23 2 (3x7y)7x=27 7 (x3y)=2 (6x5y)25 11y6 (3x2y)=22 x=5y7 3 (2xy)=4 (x3)24 3 (3xy)=5 (2x3y)15 y=3x5 4x3y=2 (7xy)10 7 (6x1)3 (8y5)=4 2 (5x2y)=3 (4xy)11 4x7y=13 2 (4x3y)=7 (xy)8 3 (x1)=2 (2y9)6 5 (x4y)=2 (2x6y7)13 4x11y=5 (2x3y2)4 5 (2xy7)=2x3y9 7xy5=3 (3x4y14)4 8x=2




追車子 3




1 4 聯立方程式 題型解析on Vimeo
4 連立一次方程式(反復法) 実用的なプログラムでは,非常に大きな連立方程式を計算しなくてはならない.数百万元 に及ぶことも珍しくない.これを,ガウス・ジョルダン法で 計算するの時間的にほとんど不可能である.そこで,これよりは格段に計算の速い方法が 用いられる.ここでは上の連立方程式の解は,x=3,y=5である。 したがって,Q 2 では,3人がけを3列,2人がけを5列使う座り方になる。 次のx,y の値の組の中で,連立方程式 5x+3y=1 7x-2y= ⎧ ⎜ ⎨ ⎜ ⎩ の解はどれですか。 ㋐ x=-1,y=2 ㋑ =-4,y=1三角方程式を解く sin x cos x = 1




4 2 3三元一次聯立方程式



國中數理輔材 Fun學練功坊數學6 二元一次聯立方程式 康軒文教 現貨 蝦皮購物
次の連立方程式を加減法で解きなさい。 解法 1 上の式と下の式を加えることで,yを消去する 方法で解きます (1) − =− = 1 5 x y x y (2) = − = 3 2 8 3 2 4 x y x y 解法 2 上の式から下の式を引くことで,xを消 去す る方法で解きます (1) − =− = 1 5 x y x y (2) = − = 3 2 8 3 2 4 x y x y213 連立代数方程式 一松 第3章 6節「連立代数方程式」の写経。 計算機代数の話題はまだ数多くあるが、近年有名になった「グレブナー基底」に ついて略説する。 多変数多項式に関する連立代数方程式を解く問題は良く現れるが、 一般的な解法はほとんどない。理論上ではつぎつぎに消去法まず次の連立方程式を解いてみましょう。これは、二元連立一次方程式です。変数(未知 数)がx とy の二つだからです。右の列に書いたものは、方程式の係数だけを取り出し て書いたものです。 と= は省いてありますが、−3 のところは、(−3) と考えて−3




トップ100連立方程式公式 最高のカラーリングのアイデア




25 3 連立方程式 ニスヌーピー壁紙
3 連立代数方程式の例題 ここで、関孝和と建部賢弘が考察した連立代数方程式を紹介しよう。 45 31 『発微算法』より 未知数を多数含む場合の連立代数方程式をどのように解いたらよいのか、それが、関ロー之が『古今算法 記』 (1670) の遺題15 問で提出した問題で、 関孝和はこの挑戦に対し4x−3y=21 (2) 「連立方程式の解」とは,左の例 (A) などにおいて2つの方程式を 両方とも満たす x , y の値のことです. 連立方程式の解を求めるには,まず,未知数が1つだけ(たとえば x だけ)の方程式を作って,解くことを考えます. x だけの方程式なら解けるからです. このように,連立方程式を解くには「未知数を1個にする」ことが鍵です.次の流れ図を




B4 2 3 演練5 已知某三元一次方程組 含有未知常數a 若方程組分別為無限多解與無解時 則a分別為多少 Youtube




高校数学 3つの解から3次方程式の作成 3変数対称式の連立方程式 受験の月




B4 2 3 三元一次方程組的加減消去法 理論 與範例1 用加減消去法解三元一次方程組 Youtube



連立方程式の行列解




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E7 B5 84 16 Pdf




第1章二元一次聯立方程式1 1 代入消去法一 章節內容 Ppt Download




Intro Linear Note
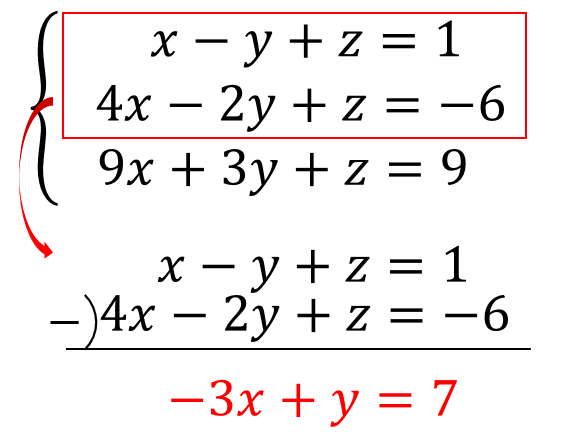



最も共有された 三連立方程式 犬イラスト




單元一二元一次聯立方程式討論一二元一次方程式 林晟數學online
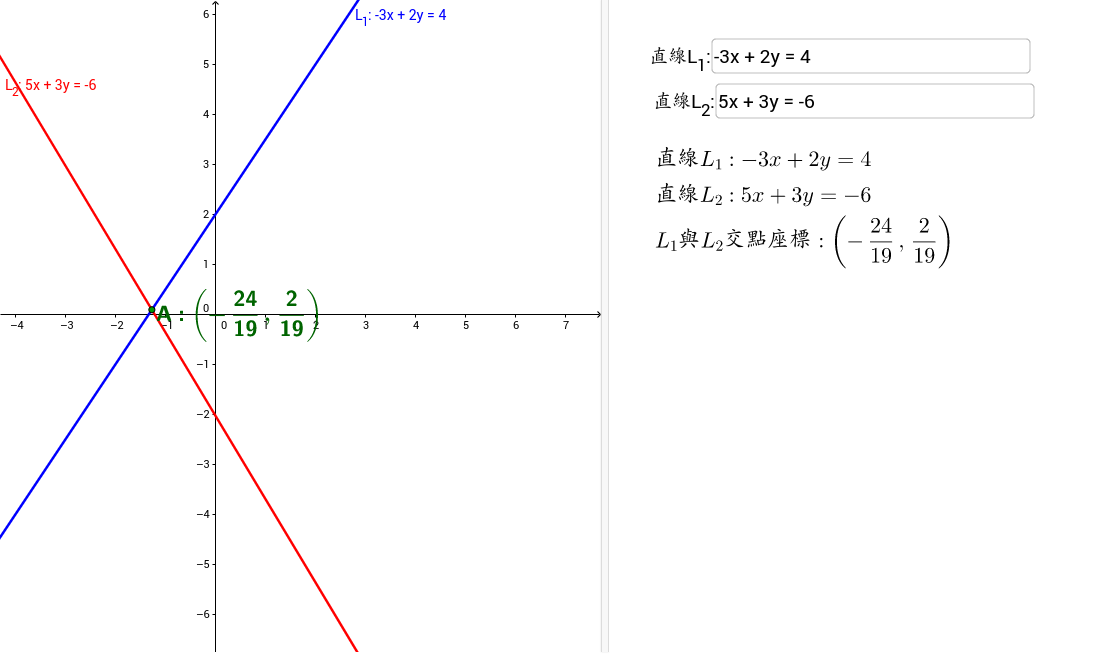



二元一次聯立方程式圖解 Geogebra




Rank Of Matrices And Homogeneous Linear Equations



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E7 B5 84 16 Pdf




連立方程式で3つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ




連立3元1次方程式 まなびの学園



Http Www Topmath Org J Student Pdf




連立方程式 3 応用編1 Youtube




三元一次連立方程式を一発で解く方法 Geogebra




怎麼知道的 紅線 Clear



Http K12 Camdemy Com Sysdata Doc 2 23e36ac63 Pdf Pdf



3 元 2 次 方程式




判斷二元一次方程式及幾組解 數學 均一教育平台




連立3元1次方程式 身勝手な主張




トップ100連立方程式公式 最高のカラーリングのアイデア



1 3 2 1 4 2 2 15r




國二junior High数学的連立方程式 筆記 Clear



1 5 聯立方程式 應用問題on Vimeo




高二高中數學的 數甲 B4 2 3 三元一次聯立方程式筆記 Clear




連立方程式 3つの文字 式の問題を計算する方法は 数スタ



測評網 國一下 數學第一次段考 複習錦囊
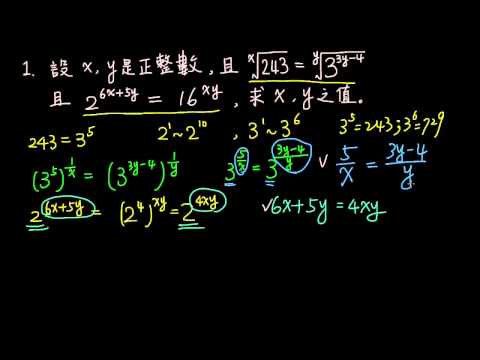



3 1進階01指數聯立方程式 指數 均一教育平台




大家來解謎 解二元一次聯立方程式 導入活動 環遊數界
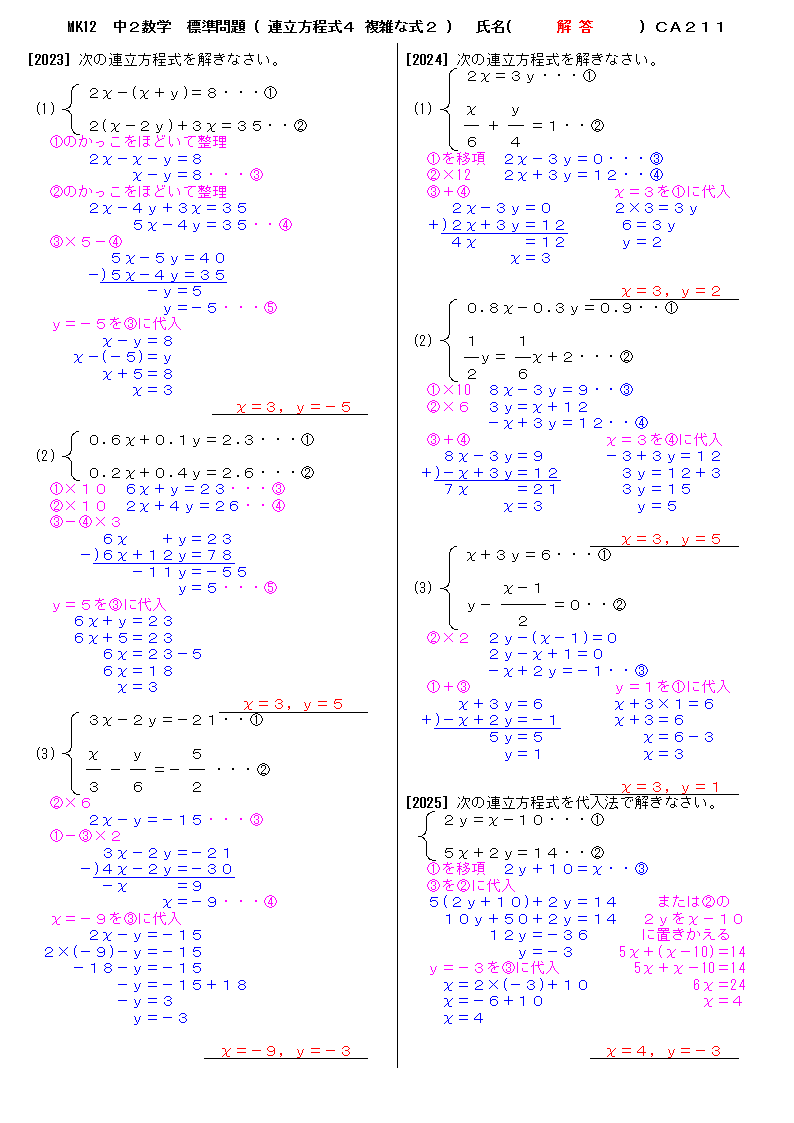



3 Y 15 Cheap Online




1 4例題3三元一次聯立方程式的無限多解 Youtube
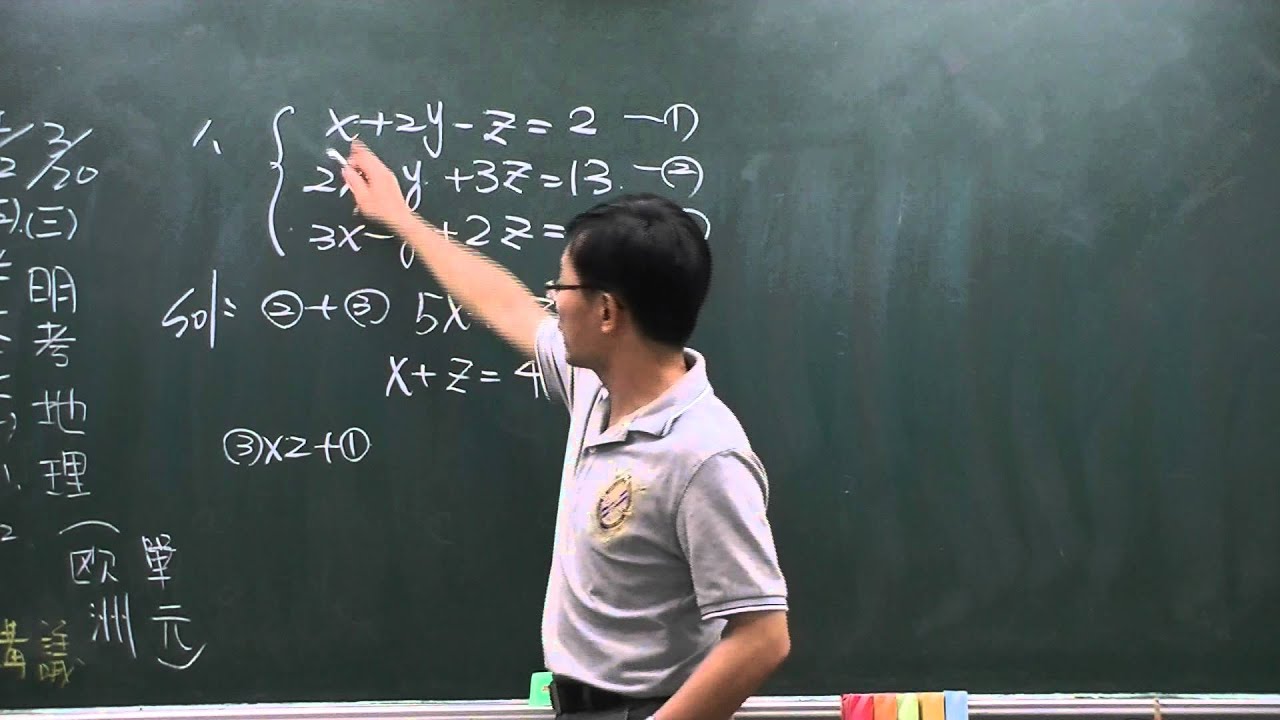



三元一次聯立方程式 解三元一次方程組 Youtube




二元一次方程组 全章复习与巩固 基础 知识讲解




三元連立方程式 1 中2数学 Youtube



名師課輔網 係數對稱的聯立方程式




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




連立方程式計算安卓下载 安卓版apk 免费下载



Q Tbn And9gctsdhxnqxebsyoonhfly Qastncurd5xayp0punpcetuujdufxx Usqp Cau




Ok423 三元一次連立方程組1 Ok423 三元一次聯立方程式主題一解聯立方程式1 可用加減消去法或代入消去法求解 2 聯立方程式的解可分成三種 1 恰有一解 2 無限多組解 3 無解 Pdf 免费下载
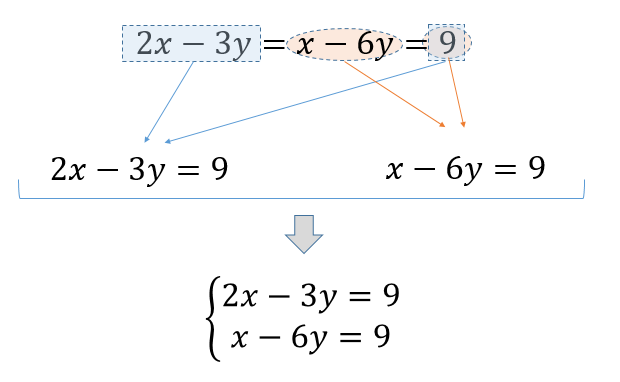



連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト




例題 連立3元1次方程式の解き方 Youtube




Rimg0010 連立方程式を解くウィルバーマシン Masakazu Takahashi Flickr



1
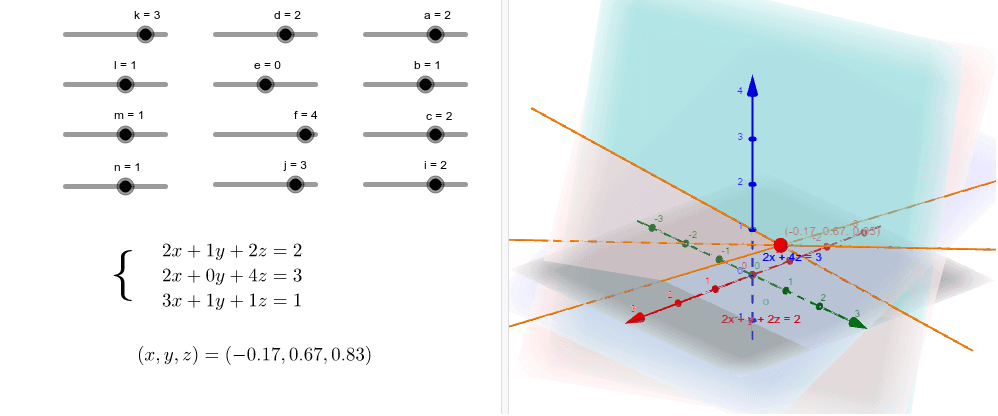



三元一次連立方程式 Geogebra




トップ100連立方程式公式 最高のカラーリングのアイデア




建宏國中e把罩數學 3 二元一次聯立方程式
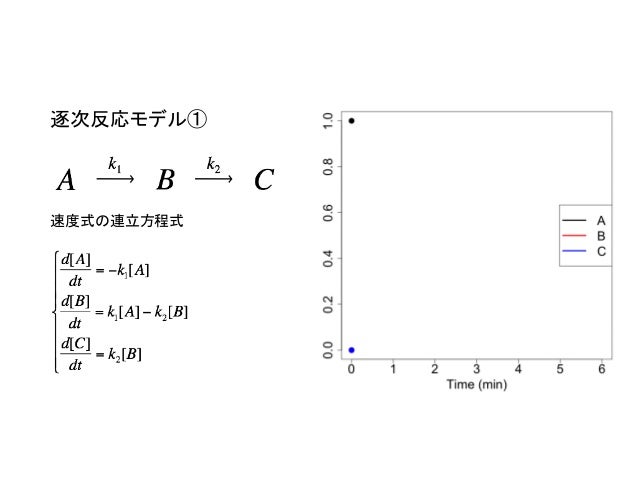



R Note Ode Ver1 0



Http Math Ymhs Tyc Edu Tw Chenjt99 Scrclass 1052 E9 Ab 98 E4 Ba 8c E9 Ab 98 E4 Ba 8c E7 Bf 92 E4 9c 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E5 8f E4 9c Pdf



連立方程式 行列計算for Android Apk Download




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




トップ100連立方程式公式 最高のカラーリングのアイデア




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E7 B5 84 16 Pdf




連立方程式の解き方 加減法 1 Youtube




二元一次聯立方程式的圖形 劉繼文 新泰國中 Shareclass




連立方程式で3つの式のある3元1次方程式とは 3元連立方程式の解き方をわかりやすく解説 Himokuri




トップ100連立方程式公式 最高のカラーリングのアイデア




連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download



1




二元二次方程式定義連立方程式とは Gjlni




1 3 2 1 4 2 2 15r




未定係数を含む3元連立方程式の解 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信




連立方程式の2つの解き方 代入法 加減法 数学fun




二元一次聯立方程式的應用題3 二元一次聯立方程式的應用問題 均一教育平台



解二元一次聯立方程式 代入消去法 Live 多媒體數學觀念典online




3 小柯以代入消去法解二元一次聯立方程式 計算步驟如下 請問小柯從哪一個步驟開 阿摩線上測驗




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download
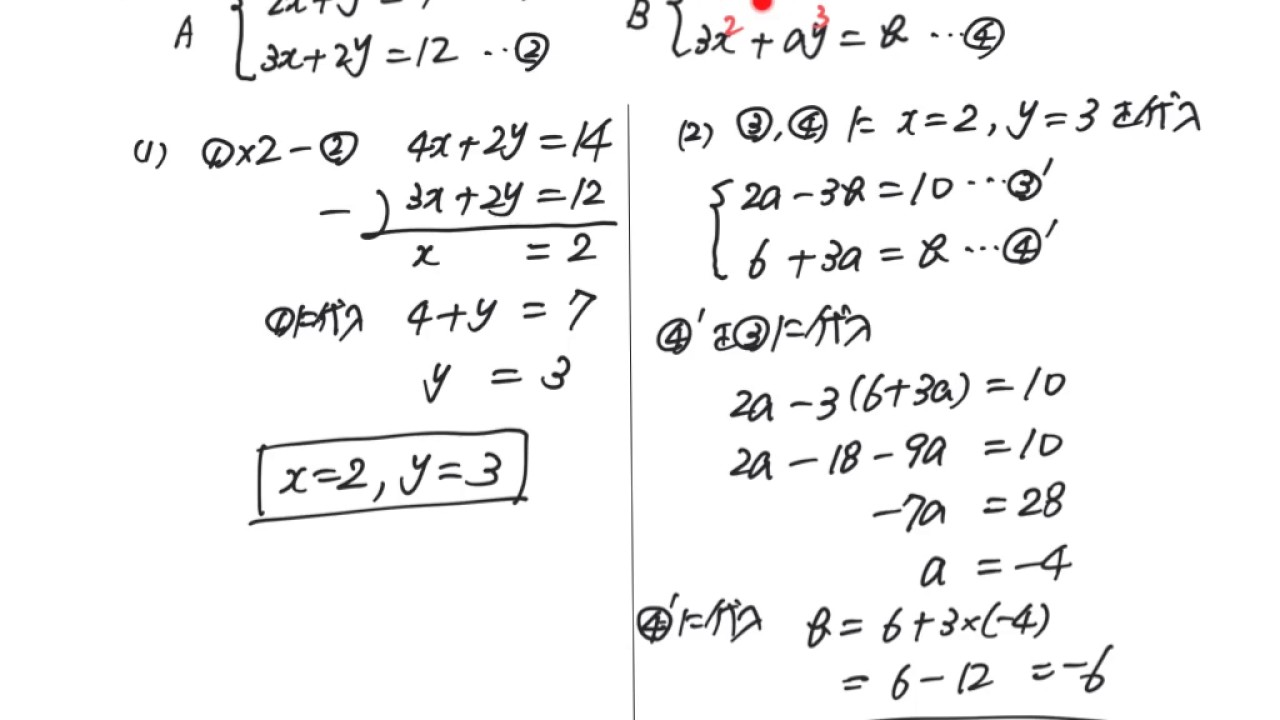



中2数学連立方程式 4つの式が同じ解を持つ Youtube




Tiktok 上的 連立方程式標籤影片




解二元一次聯立方程式綜合應用3 Youtube




3分で分かる 式が3つの連立方程式の解き方をわかりやすく解説 合格サプリ




一元三次方程式試誤法例題 三角函數 利用三角函數求解一元三次方程式 Pripdw




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



Http Jendo Org Files 6year E6 95 99 E5 Ad B8 E8 87 E6 Ba 90 E6 95 B8 E5 Ad B8 E6 95 B8 E5 Ad B8 E7 B4 E7 Bf 92 E4 Ba 8c E5 85 E4 B8 80 E6 Ac A1 E6 96 B9 E7 A8 8b E5 8f 98 Ex 7b C01 Pdf




1 3 2 1 4 2 2 15r




Intro Linear Note




ある連立3元3次方程式を解いてみよう 身勝手な主張




例題 解二元一次聯立方程式 綜合應用2 數學 均一教育平台




連立方程式 A B Cの3つ式があるときの解き方を解説 中学数学 理科の学習まとめサイト




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download



連立方程式計算 Apps On Google Play




Intro Linear Note




連立方程式で3つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ
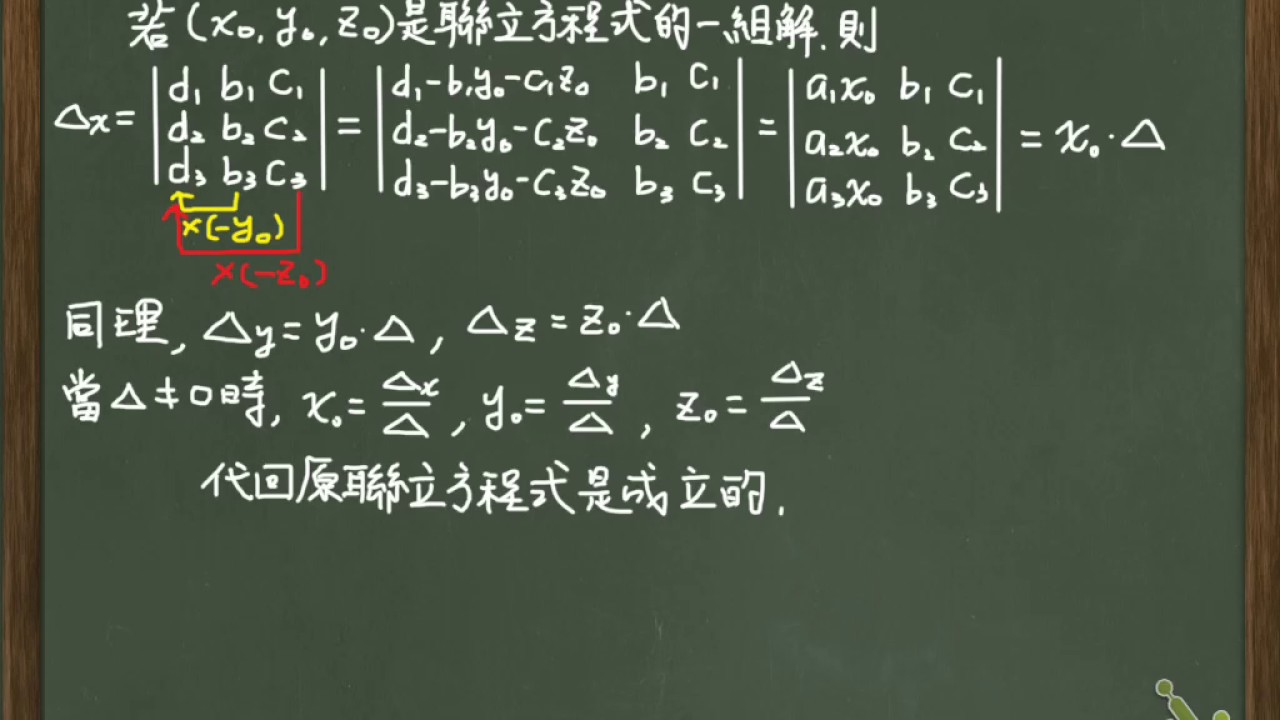



40 三元一次聯立方程式的公式解 克拉瑪公式的說明 Youtube



1
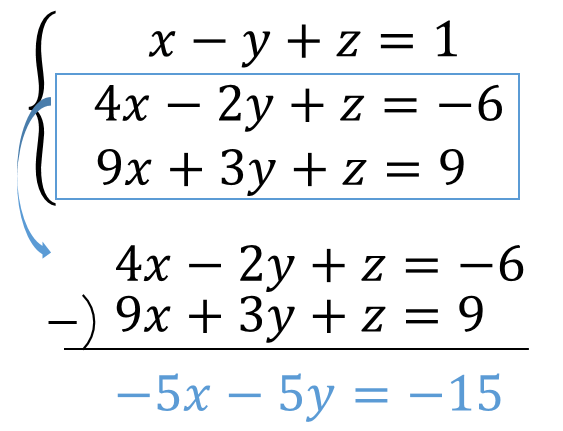



連立方程式 3つの文字 式の問題を計算する方法は 数スタ



0 件のコメント:
コメントを投稿